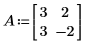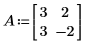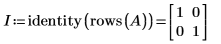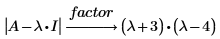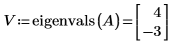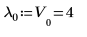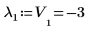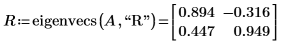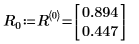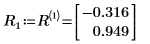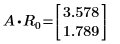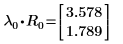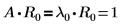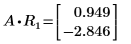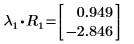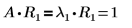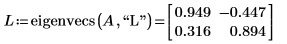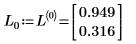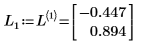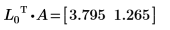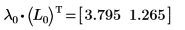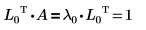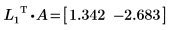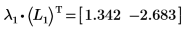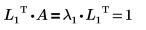Exemple : Recherche des vecteurs propres gauche et droite
Pour éviter les incohérences lors de comparaisons booléennes, activez Egalité approximative dans la liste déroulante Options de calcul.
1. Définissez une matrice carrée réelle.
2. Utilisez la définition de base d'eigenval pour trouver les lambdas de la matrice A.
3. Sinon, utilisez la fonction eigenvals pour trouver les lambdas de la matrice A.
Recherche des vecteurs propres de droite
1. Utilisez la fonction eigenvecs pour rechercher les vecteurs propres de droite (par défaut) de la matrice A.
2. Montrez que la relation A x Rn = λn x Rn est vraie.
Les relations sont vraies.
Recherche des vecteurs propres de gauche
1. Utilisez la fonction eigenvecs pour rechercher les vecteurs propres de gauche de la matrice A.
2. Montrez que la relation LnT x A = λn x LnT est vraie.
La relation est vraie.