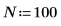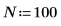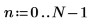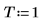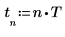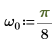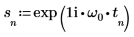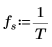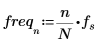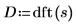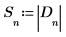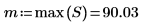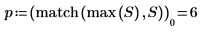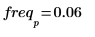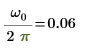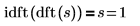Exemple : DFT de fonctions complexes
Utilisez les fonctions dft et idft pour calculer la transformée de Fourier complexe ou ascendante avancée ou la transformée de Fourier inverse.
1. Créez quelques données complexes simulées avec N points de données.
2. Définissez l'espacement d'échantillonnage.
3. Utilisez la fonction exp pour définir le signal suivant.
4. Définissez la fréquence d'échantillonnage et la fréquence qui correspond à la nième entrée dans le vecteur transformé.
5. Appliquez la fonction dft pour transformer les données en domaine de fréquences.
6. Enregistrez l'amplitude des éléments du tableau D dans un nouveau tableau.
7. Utilisez les fonctions match et max pour calculer l'amplitude et la fréquence du pic.
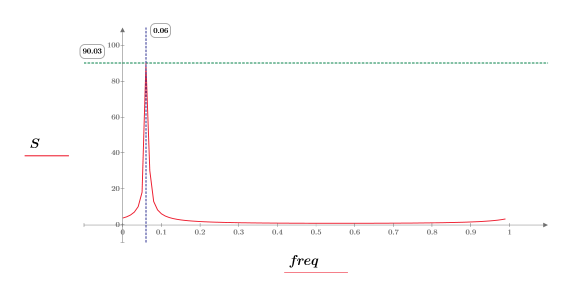
8. Tracez l'amplitude de DFT comme une fonction de la fréquence.
9. Démontrez que la fréquence de la valeur pic correspond à ω0/2π.
10. Utilisez la fonction idft pour démontrer que la IDFT de TFD d'un signal renvoie le signal lui-même.