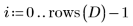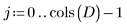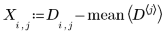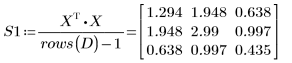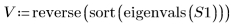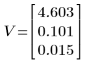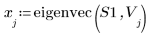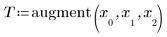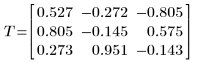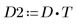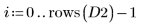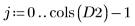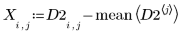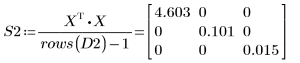Exemple : Analyse de composant principal et de covariance
Calculez la covariance d'un jeu de données et utilisez les fonctions eigenvals et eigenvec pour effectuer l'analyse de composant principal.
1. Définissez la matrice suivante D.
Chaque ligne de D représente une observation, chaque colonne une caractéristique mesurée.
2. Calculez la matrice de covariance de l'échantillon.
3. Calculez et triez les valeurs propres.
4. Calculez la matrice de transformation.
5. Transformez les données d'origine.
6. Calculez la matrice de covariance des données transformées.
Les principaux composants des données sont les éléments diagonaux de la matrice S2.