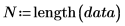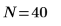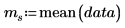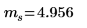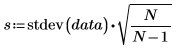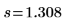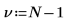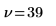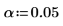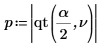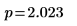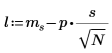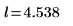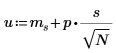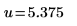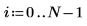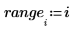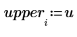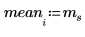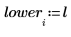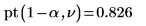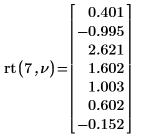Exemple : Intervalle de confiance pour la moyenne
Calculez un intervalle de confiance permettant d'estimer la moyenne d'une population normale lorsque la variation de cette dernière est inconnue.
1. Définissez un exemple d'ensemble de données
2. Utilisez les fonctions length, mean, et stdev pour collecter des exemples de statistiques.
Nombre d'échantillons | | |
Moyenne de l'échantillon | | |
Ecart-type de l'échantillon | | |
Degrés de liberté | | |
3. Entrez le niveau de signification bilatéral :
Il équivaut à un intervalle de confiance de 95 %.
4. Utilisez la fonction qt pour calculer le 95e centile de la loi T de Student pour un test bilatéral.
5. Calculez les limites inférieure et supérieure de l'intervalle de confiance.
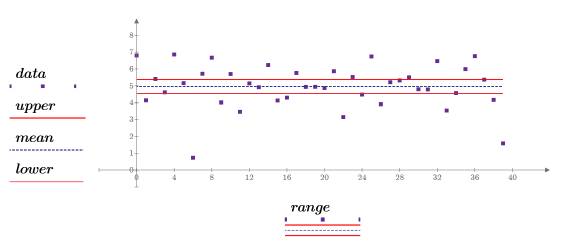
6. Tracez l'exemple de données, sa moyenne et son intervalle de confiance.
7. Utilisez la fonction pt pour calculer la fonction de répartition de la loi de probabilité pour l'intervalle de confiance :
8. Utilisez la fonction rt pour créer un vecteur des nombres aléatoires ayant une loi T de Student :
Lorsque vous recalculez le document, la fonction rt restitue un autre ensemble de nombres aléatoires.