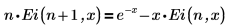Exponential Integrals
• Ei(x)—Returns the exponential integral function (Cauchy principal value) of x, which is defined as follows:
Ei(x) returns only the real part of the complex exponential integral function.
For x > 0, the integral is interpreted as the Cauchy principal value.
• Ei(n, x)—Returns the generalized exponential integral function of x.
For an arbitrary integer n, Ei(n, x) is defined by the recurrence relation:
For the case of n = 1, Ei(n, x) is defined as follows:
where γ is Euler's constant.
For a real number x, Ei(x) and Ei(n, x) are related to each other as follows:
Arguments
• x is a real scalar, a vector, or a square matrix. When using the generalized exponential integral function, x can also be complex scalar.
• n is a real or complex scalar.