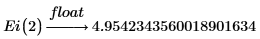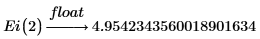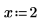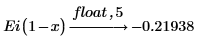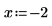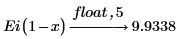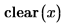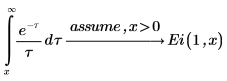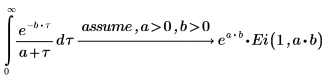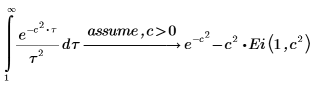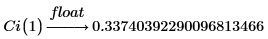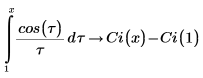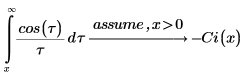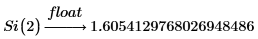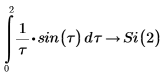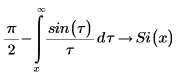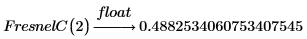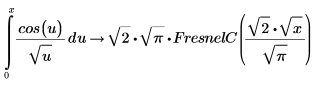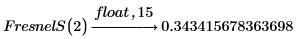Example: Symbolic Integral Functions
Use the keyword float to evaluate functions that can only be evaluated with the symbolic equal sign, and not with the numerical equal sign.
Ei: Exponential Integral
1. Use the keyword float to evaluate function Ei numerically at x=2:
2. Evaluate the complex exponential integral function for a real number x:
3. Use function clear to clear the previous numeric and symbolic value of x:
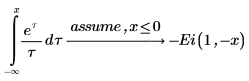
4. Verify that the following integrals return answers in terms of the exponential integral function:
Ci: Cosine Integral
1. Use the keyword float to evaluate function Ci at x=1:
2. Verify that the following integrals return answers in terms of the cosine integral function:
Si: Sine Integral
1. Use the keyword float to evaluate function Si at x=2:
2. Verify that the following integrals return answers in terms of the sine integral function:
FresnelC: Fresnel Cosine Integral
1. Use the keyword float to evaluate function FresnelC at x=2:
2. Verify that the following integral returns an answer in terms of the Fresnel cosine integral function:
FresnelS: Fresnel Sine Integral
1. Use the keyword float to evaluate function FresnelS at x=2:
2. Verify that the following integral returns a result in terms of the Fresnel sine and Fresnel cosine integrals: