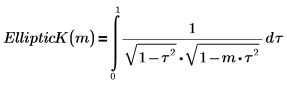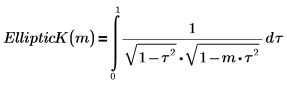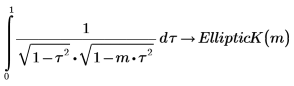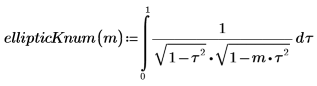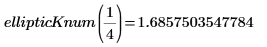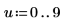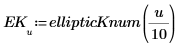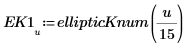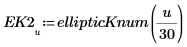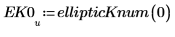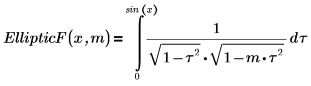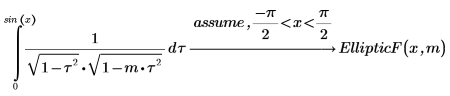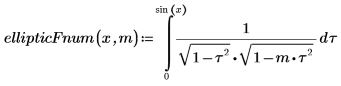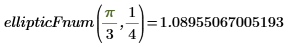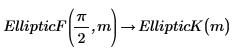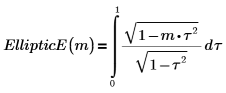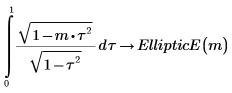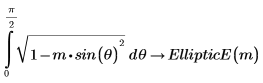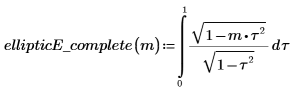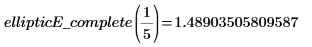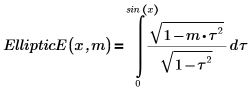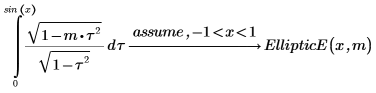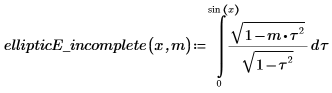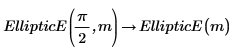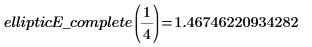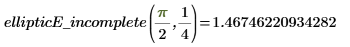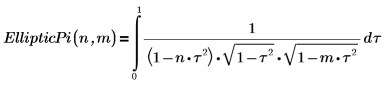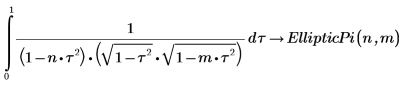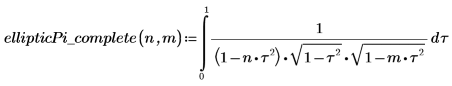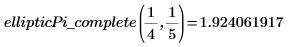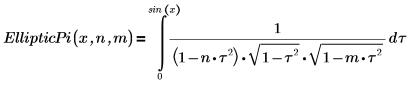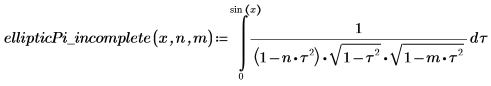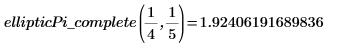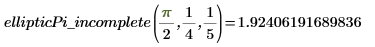Exemple : Fonctions intégrales elliptiques symboliques
Les fonctions intégrales elliptiques suivantes apparaissent dans de nombreux calculs symboliques.
EllipticK : intégrale elliptique complète du premier type
1. Affichez la définition de l'intégrale elliptique complète du premier type, EllipticK(m).
2. Définissez une fonction qui calcule l'intégrale ci-dessus.
3. Evaluez la fonction EllipticK complète de manière numérique.
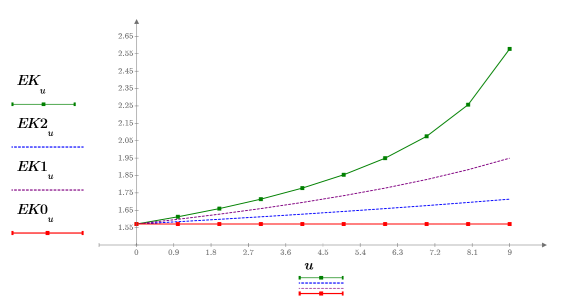
4. Tracez les valeurs numériques de la fonction EllipticK pour les valeurs 0 ≤ m < 1.0.
L'intégrale est égale à zéro lorsque m=0, et elle approche l'infini lorsque m s'approche de 1.
EllipticF : intégrale elliptique incomplète du premier type
1. Affichez la définition de l'intégrale elliptique incomplète du premier type, EllipticF(x, m).
2. Définissez une fonction qui calcule l'intégrale ci-dessus.
3. Evaluez l'intégrale EllipticF incomplète de manière numérique.
4. Affichez la relation entre les intégrales EllipticK et EllipticF.
EllipticE : intégrales elliptiques complète et incomplète du deuxième type
1. Affichez la définition de l'intégrale elliptique complète du deuxième type, EllipticE(m).
La fonction est également donnée par la définition suivante :
2. Définissez une fonction qui calcule l'intégrale ci-dessus.
3. Evaluez la fonction EllipticE complète de manière numérique.
4. Affichez la définition de l'intégrale elliptique incomplète du deuxième type, EllipticE(x, m).
5. Définissez une fonction qui calcule l'intégrale ci-dessus.
6. Affichez la relation entre les intégrales complète et incomplète EllipticE.
7. Evaluez les intégrales complète et incomplète EllipticE de manière numérique.
EllipticPi : intégrales elliptiques complète et incomplète du troisième type
1. Affichez la définition de l'intégrale elliptique complète du troisième type, EllipticPi(n, m).
2. Définissez une fonction qui calcule l'intégrale ci-dessus.
3. Evaluez l'intégrale EllipticPi complète de manière numérique.
4. Affichez la définition de l'intégrale elliptique incomplète du troisième type, EllipticPi(x, n, m).
5. Définissez une fonction qui calcule l'intégrale ci-dessus.
6. Evaluez l'intégrale EllipticPi de manière numérique.