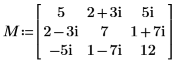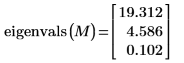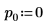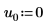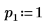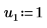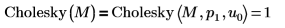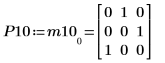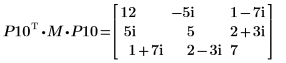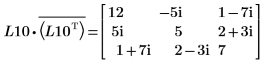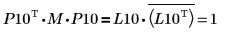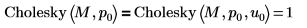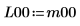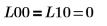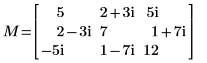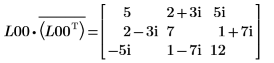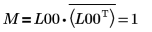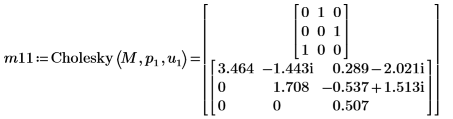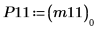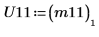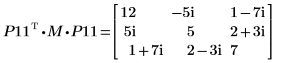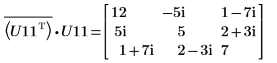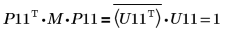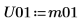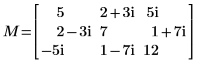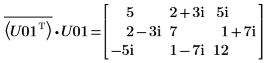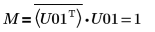Exemple : Factorisation de Cholesky des matrices complexes
Utilisez la fonction Cholesky pour effectuer la factorisation Cholesky d'une matrice Hermitian complexe.
|
|
Pour éviter les incohérences lors de comparaisons booléennes, activez Egalité approximative dans la liste déroulante Options de calcul.
|
1. Définissez une matrice carrée définie Hermitian complexe M.
2. Appliquez la fonction eigenvals pour vous assurer que la matrice est positive définie.
3. Définissez les arguments p et u pour contrôler l'activation/la désactivation du pivotement et la factorisation inférieure/supérieure.
4. Utilisez la fonction Cholesky pour effectuer la factorisation par défaut de la matrice M, avec pivotement et factorisation inférieure.
| La fonction par défaut Cholesky(M) est équivalente à Cholesky(M,1,0) |
5. Montrez que P10T x M x P10 = L10 x conj(L10T).
La relation est logiquement vraie.
6. Utilisez la fonction Cholesky pour effectuer la factorisation par défaut de la matrice M, sans pivotement ni factorisation inférieure (par défaut).
| Ne pas spécifier d'argument u, comme dans Cholesky(M, 0), équivaut à la définir sur 0 comme dans Cholesky(M, 0, 0). |
| Lorsque le pivotement est activé, la matrice inférieure renvoyée, L10, n'est PAS égale à la matrice inférieure renvoyée, L00, lorsqu'il est désactivé. La relation est logiquement fausse. |
7. Montrez que M = L00 x conj(L00T).
La relation est logiquement vraie.
8. Utilisez la fonction Cholesky pour effectuer la factorisation de la matrice M, avec pivotement et factorisation supérieure.
9. Montrez que P11T x M x P11 = conj(U11T) x U11.
La relation est logiquement vraie.
10. Utilisez la fonction Cholesky pour effectuer la factorisation de la matrice M, sans pivotement ni factorisation supérieure.
11. Montrez que M = conj(U01T) x U01.
La relation est logiquement vraie.