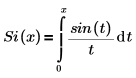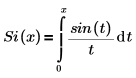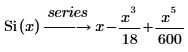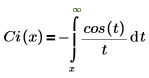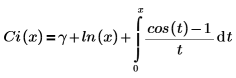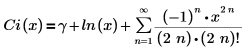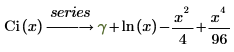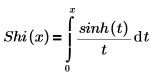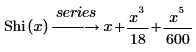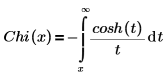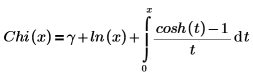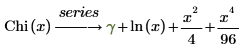Sine and Cosine Integrals
• Si(x)—The Sine integral function is defined as:
The series expansion representation is:
The first six terms of the series are:
• Ci(x)—The Cosine integral function is defined as:
Another form of the definition is:
The series expansion representation is:
The first six terms of the series are:
• Shi(x)—The Hyperbolic sine integral function is defined as:
The first six terms of the series are:
The terms of the series expansion of the Si and Shi functions are identical except for the sign of the terms where n is even.
• Chi(x)—The Hyperbolic cosine integral function is defined as:
Another form of the definition is:
The first six terms of the series are:
The terms of the series expansion of the Ci and Chi functions are identical except for the sign of the terms where n is odd.
Arguments
• x is a real or complex scalar, or a vector of real or complex scalars.
Additional Information
These functions are useful with using the float keyword that numerically evaluates functions instead of returning symbolic math.