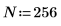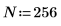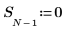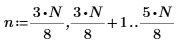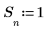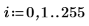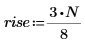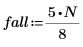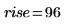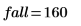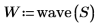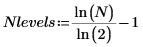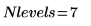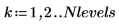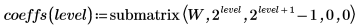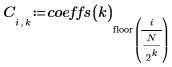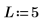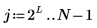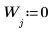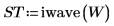Example: Wavelet Transforms
Use the wavelet transform functions for compressing data.
1. Define a single square wave signal, where:
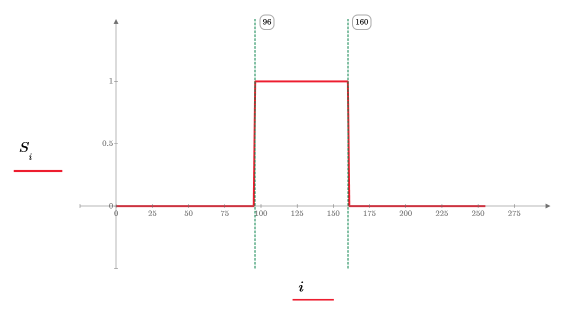
2. Evaluate array n and plot signal S:
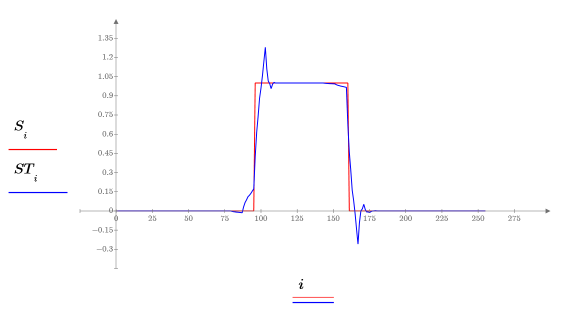
Over the range of 0..255, signal S has an amplitude of 1 for all values of n (96..160), and an amplitude of zero otherwise.
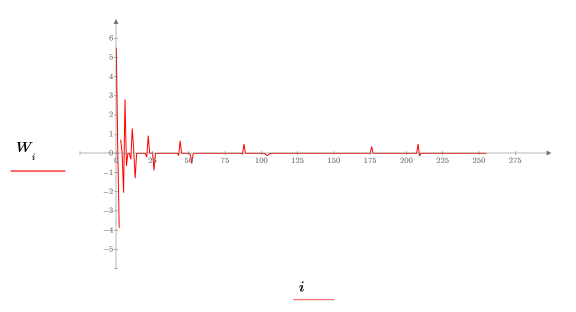
3. Use the wave function to calculate the Wavelet transform of signal S:
4. Calculate the number of levels contained in this transform:
5. Use functions submatrix and floor in order to obtain a sense of the relative importance of each level:
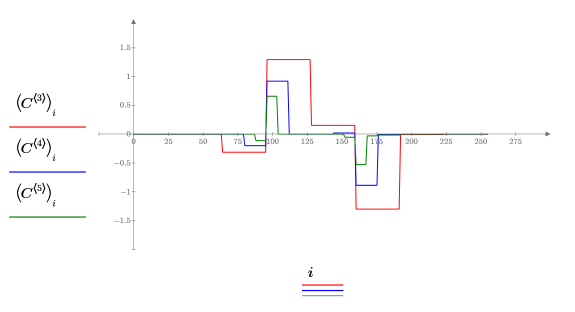
6. Plot several levels of coefficients simultaneously:
7. Represent signal with less data, by doing two things:
a. Zero out the higher level coefficients
b. Compute the inverse wavelet transform of the new coefficient vectors
First level at which coefficients are set to zero (L < 7 may be varied).
8. Use function iwave to recover the original signal:
9. Plot and compare the original signal with the transformed signal:
This technique offers a way of compressing the data needed to represent a signal.