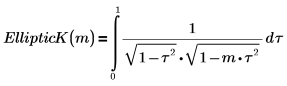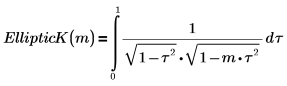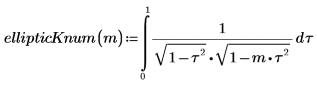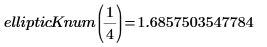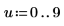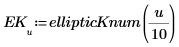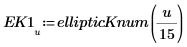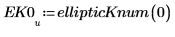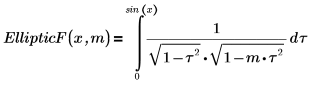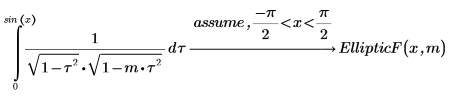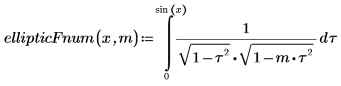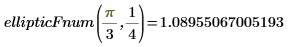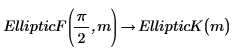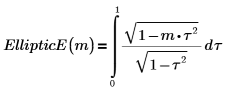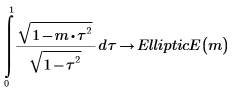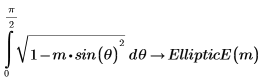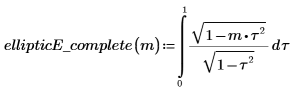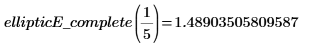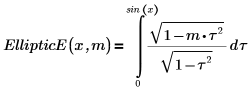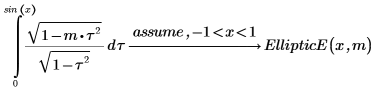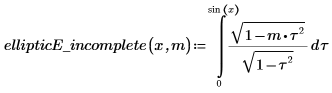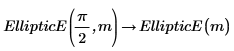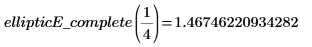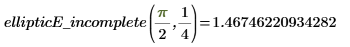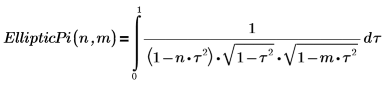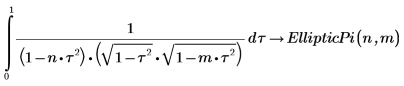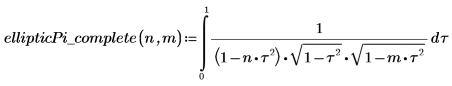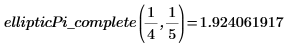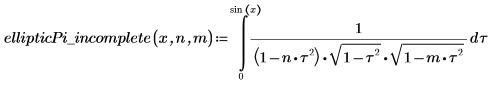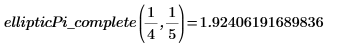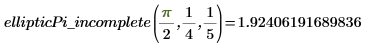Example: Symbolic Elliptic Integral Functions
The following elliptic integral functions appear in many symbolic calculations.
EllipticK: Complete Elliptic Integral of the First Kind
1. Show the definition of the complete elliptic integral of the first kind, EllipticK(m).
2. Define a function that computes the above integral.
3. Evaluate the complete EllipticK numerically.
4. Plot the numerical values of EllipticK for values of 0 ≤ m < 1.0.
The integral equals zero when m=0, and it approaches infinity as m approaches 1.
EllipticF: Incomplete Elliptic Integral of the First Kind
1. Show the definition of the incomplete elliptic integral of the first kind, EllipticF(x, m).
2. Define a function that computes the above integral.
3. Evaluate the incomplete EllipticF integral numerically.
4. Show the relationship between the EllipticK and EllipticF integrals.
EllipticE: Complete and Incomplete Elliptic Integral of the Second Kind
1. Show the definition of the complete elliptic integral of the second kind, EllipticE(m).
Alternatively, the function is given by the following definition:
2. Define a function that computes the above integral.
3. Evaluate the complete EllipticE numerically.
4. Show the definition of the incomplete elliptic integral of the second kind, EllipticE(x, m).
5. Define a function that computes the above integral
6. Show the relationship between the complete and incomplete EllipticE integrals.
7. Evaluate the complete and incomplete EllipticE integrals numerically.
EllipticPi: Complete and Incomplete Elliptic Integrals of the Third Kind
1. Show the definition of the complete elliptic integral of the third kind, EllipticPi(n, m).
2. Define a function that computes the above integral.
3. Evaluate the complete EllipticPi integral numerically.
4. Show the definition of the incomplete elliptic integral of the third kind, EllipticPi(x, n, m).
5. Define a function that computes the above integral.
6. Evaluate the EllipticPi integral numerically.