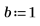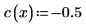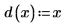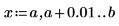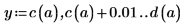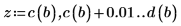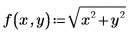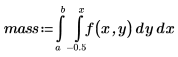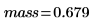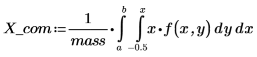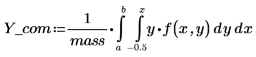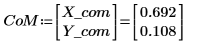Example: Numerical Double Integrals
Evaluate integrals of a real-valued function over a region in the x-y plane to calculate the mass and the center of mass over that region.
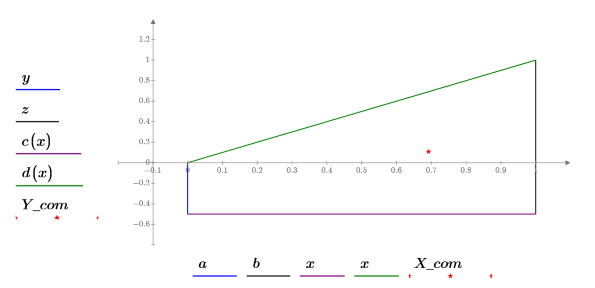
1. Define the boundaries of the region over which to evaluate the integrals. Let a < x < b and c(x) < y < d(x) for all x.
2. Plot the region over which to evaluate the integrals.
3. Define the real-valued function to integrate.
Function f(x, y) is the density at point (x, y). It is proportional to the distance between the point and the origin.
4. Find the mass inside the defined region.
5. Find the location of the center of mass CoM.
6. Show CoM on the previous plot