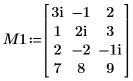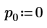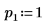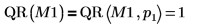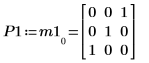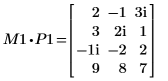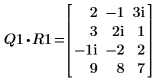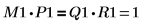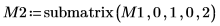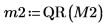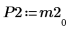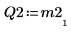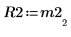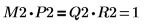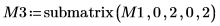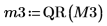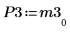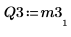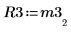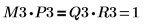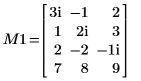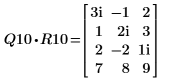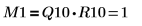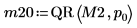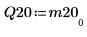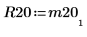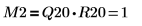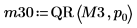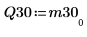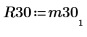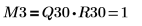Example: QR Matrix Factorization
Use the QR function to perform QR matrix factorization.
|
|
• To avoid logical mismatches when performing boolean comparisons, enable Approximate Equality in the Calculation Options drop-down list.
• The example uses a complex matrix as input, but the function also accepts a real matrix as input.
|
QR Factorization with Pivoting
1. Define a real matrix M1 of dimensions m x n such that m > n.
2. Set argument p to control the enabling/disabling of pivoting.
3. Use the QR function to perform QR matrix factorization of matrix M1.
| The default function QR(M1) is equivalent to QR(M,1). |
4. Show that M1 x P1 = Q1 x R1.
| |
| |
The relationship is logically true. | |
5. Use the submatrix function to extract matrix M2, such that m < n, then apply the QR function.
6. Show that M2 x P2 = Q2 x R2.
| | |
| | |
The relationship is logically true. |
7. Use the submatrix function to extract matrix M3, such that m = n, then apply the QR function.
8. Show that M3 x P3 = Q3 x R3.
| | |
| | |
The relationship is logically true. | | |
QR Factorization with No Pivoting
1. Disable pivoting then apply the QR function to matrix M1 (m > n).
2. Show that M1 = Q10 x R10.
| |
| |
The relationship is logically true. |
3. Disable pivoting then apply the QR function to matrix M2 (m < n).
4. Show that M2 = Q20 x R20.
| |
| |
The relationship is logically true. |
5. Disable pivoting then apply the QR function to matrix M3 (m = n).
6. Show that M3 = Q30 x R30.
| |
| |
The relationship is logically true. |