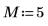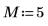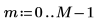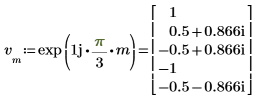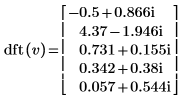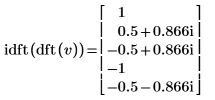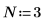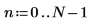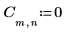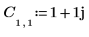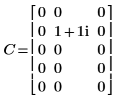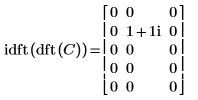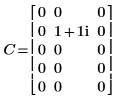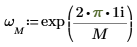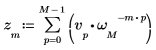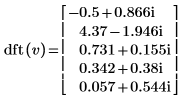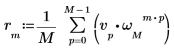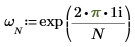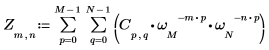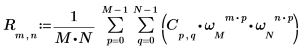Example: The Inverse Transformation idft

Functions > Transforms and Filters > Example: The Inverse Transformation idft

Example: The Inverse Transformation idft

The idft function is the inverse transform of dft and therefore it is expected to restore the original data input to the complex transform.

Working with Vectors (1D)

1. Define the length of vector v.

Click to copy this expression

Click to copy this expression

2. Use the exp function to define and evaluate vector v.

Click to copy this expression

<region id="ID0EWHDCB" top="307.20000000000005" left="38.400000000000006" actualWidth="265.80333333333328" actualHeight="100" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="210">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <indexer />
        <id labels="VARIABLE" xml:space="preserve">v</id>
        <id labels="*" xml:space="preserve">m</id>
      </apply>
      <eval>
        <apply>
          <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">exp</id>
          <apply>
            <mult />
            <apply>
              <mult />
              <imag symbol="j">1</imag>
              <apply>
                <div />
                <id labels="CONSTANT" xml:space="preserve" label-is-contextual="true">π</id>
                <real>3</real>
              </apply>
            </apply>
            <id xml:space="preserve">m</id>
          </apply>
        </apply>
        <unitOverride>
          <placeholder />
        </unitOverride>
      </eval>
    </define>
    <resultFormat>
      <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

3. Use the dft function to calculate the forward transform of vector v.

Click to copy this expression

4. Use the idft function to calculate the inverse transform of vector v.

Click to copy this expression

5. Show that the inverse transform of the forward transform of vector v is the original vector v.

Click to copy this expression

Click to copy this expression

The results are identical.

Working with Matrices (2D)

1. Define and evaluate matrix C.

Click to copy this expression

Click to copy this expression

Click to copy this expression

Click to copy this expression

Click to copy this expression

2. Use the dft function to calculate the forward transform of matrix C.

Click to copy this expression

3. Use the idft function to calculate the inverse transform of matrix C.

Click to copy this expression

4. Show that the inverse transform of the forward transform of matrix C is the original matrix C.

Click to copy this expression

Click to copy this expression

The results are identical.

Demonstrating the Underlying Sum Behind idft

One-dimensional Case:

1. Use the exp function and the sum operator to calculate the inverse transform of vector v.

Click to copy this expression

Click to copy this expression

<region id="ID0EH3DCB" top="1843.2000000000003" left="38.400000000000006" actualWidth="155.60999999999999" actualHeight="50.000000000000007" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="240">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <indexer />
        <id labels="VARIABLE" xml:space="preserve">z</id>
        <id labels="*" xml:space="preserve">m</id>
      </apply>
      <apply>
        <summation />
        <lambda>
          <boundVars>
            <id xml:space="preserve">p</id>
          </boundVars>
          <parens>
            <apply>
              <mult />
              <apply>
                <indexer />
                <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">v</id>
                <id xml:space="preserve">p</id>
              </apply>
              <apply>
                <pow />
                <apply>
                  <indexer />
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">ω</id>
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M</id>
                </apply>
                <apply>
                  <mult />
                  <apply>
                    <neg />
                    <id xml:space="preserve">m</id>
                  </apply>
                  <id xml:space="preserve">p</id>
                </apply>
              </apply>
            </apply>
          </parens>
        </lambda>
        <lowerBound>
          <real>0</real>
        </lowerBound>
        <upperBound>
          <apply>
            <minus />
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M</id>
            <real>1</real>
          </apply>
        </upperBound>
      </apply>
    </define>
    <resultFormat>
      <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

2. Compare the resulting forward transform of vector v with the output of the dft function.

Click to copy this expression

Click to copy this expression

The results are identical.

3. Use the sum operator to calculate the inverse transform of vector v.

Click to copy this expression

<region id="ID0EFBECB" top="2112.0000000000005" left="38.400000000000006" actualWidth="173.77666666666664" actualHeight="50.75866666666667" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="246">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <indexer />
        <id labels="VARIABLE" xml:space="preserve">r</id>
        <id labels="*" xml:space="preserve">m</id>
      </apply>
      <apply>
        <scale />
        <apply>
          <div />
          <real>1</real>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M</id>
        </apply>
        <apply>
          <summation />
          <lambda>
            <boundVars>
              <id xml:space="preserve">p</id>
            </boundVars>
            <parens>
              <apply>
                <mult />
                <apply>
                  <indexer />
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">v</id>
                  <id xml:space="preserve">p</id>
                </apply>
                <apply>
                  <pow />
                  <apply>
                    <indexer />
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">ω</id>
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M</id>
                  </apply>
                  <apply>
                    <mult />
                    <id xml:space="preserve">m</id>
                    <id xml:space="preserve">p</id>
                  </apply>
                </apply>
              </apply>
            </parens>
          </lambda>
          <lowerBound>
            <real>0</real>
          </lowerBound>
          <upperBound>
            <apply>
              <minus />
              <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M</id>
              <real>1</real>
            </apply>
          </upperBound>
        </apply>
      </apply>
    </define>
    <resultFormat>
      <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

4. Compare the resulting inverse transform of vector v with the output of the idft function.

Click to copy this expression

Click to copy this expression

The results are identical.

Two-dimensional case:

1. Use the exp function and the sum operator to calculate the forward transform of matrix C.

Click to copy this expression

<region id="ID0EPGECB" top="2419.2000000000003" left="38.400000000000006" actualWidth="135.11" actualHeight="47.2" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="252">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <indexer />
        <id labels="VARIABLE" xml:space="preserve">ω</id>
        <id labels="*" xml:space="preserve">N</id>
      </apply>
      <apply>
        <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">exp</id>
        <apply>
          <div />
          <apply>
            <mult />
            <apply>
              <mult />
              <real>2</real>
              <id labels="CONSTANT" xml:space="preserve">π</id>
            </apply>
            <imag symbol="i">1</imag>
          </apply>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">N</id>
        </apply>
      </apply>
    </define>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

Click to copy this expression

<region id="ID0E6GECB" top="2476.8" left="38.400000000000006" actualWidth="269.42666666666673" actualHeight="50.000000000000007" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="254">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <indexer />
        <id labels="VARIABLE" xml:space="preserve">Z</id>
        <sequence>
          <id labels="*" xml:space="preserve">m</id>
          <id labels="*" xml:space="preserve">n</id>
        </sequence>
      </apply>
      <apply>
        <summation />
        <lambda>
          <boundVars>
            <id xml:space="preserve">p</id>
          </boundVars>
          <apply>
            <summation />
            <lambda>
              <boundVars>
                <id xml:space="preserve">q</id>
              </boundVars>
              <parens>
                <apply>
                  <mult />
                  <apply>
                    <mult />
                    <apply>
                      <indexer />
                      <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">C</id>
                      <sequence>
                        <id xml:space="preserve">p</id>
                        <id xml:space="preserve">q</id>
                      </sequence>
                    </apply>
                    <apply>
                      <pow />
                      <apply>
                        <indexer />
                        <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">ω</id>
                        <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M</id>
                      </apply>
                      <apply>
                        <mult />
                        <apply>
                          <neg />
                          <id xml:space="preserve">m</id>
                        </apply>
                        <id xml:space="preserve">p</id>
                      </apply>
                    </apply>
                  </apply>
                  <apply>
                    <pow />
                    <apply>
                      <indexer />
                      <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">ω</id>
                      <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">N</id>
                    </apply>
                    <apply>
                      <mult />
                      <apply>
                        <neg />
                        <id xml:space="preserve">n</id>
                      </apply>
                      <id xml:space="preserve">p</id>
                    </apply>
                  </apply>
                </apply>
              </parens>
            </lambda>
            <lowerBound>
              <real>0</real>
            </lowerBound>
            <upperBound>
              <apply>
                <minus />
                <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">N</id>
                <real>1</real>
              </apply>
            </upperBound>
          </apply>
        </lambda>
        <lowerBound>
          <real>0</real>
        </lowerBound>
        <upperBound>
          <apply>
            <minus />
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M</id>
            <real>1</real>
          </apply>
        </upperBound>
      </apply>
    </define>
    <resultFormat>
      <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

2. Compare the resulting forward transform of matrix C with the output of the dft function.

Click to copy this expression

Click to copy this expression

The results are identical.

3. Use the sum operator to calculate the inverse transform of matrix C.

Click to copy this expression

<region id="ID0EBLECB" top="2918.4000000000005" left="38.400000000000006" actualWidth="303.16333333333336" actualHeight="50.75866666666667" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="260">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <indexer />
        <id labels="VARIABLE" xml:space="preserve">R</id>
        <sequence>
          <id labels="*" xml:space="preserve">m</id>
          <id labels="*" xml:space="preserve">n</id>
        </sequence>
      </apply>
      <apply>
        <scale />
        <apply>
          <div />
          <real>1</real>
          <apply>
            <mult />
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M</id>
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">N</id>
          </apply>
        </apply>
        <apply>
          <summation />
          <lambda>
            <boundVars>
              <id xml:space="preserve">p</id>
            </boundVars>
            <apply>
              <summation />
              <lambda>
                <boundVars>
                  <id xml:space="preserve">q</id>
                </boundVars>
                <parens>
                  <apply>
                    <mult />
                    <apply>
                      <mult />
                      <apply>
                        <indexer />
                        <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">C</id>
                        <sequence>
                          <id xml:space="preserve">p</id>
                          <id xml:space="preserve">q</id>
                        </sequence>
                      </apply>
                      <apply>
                        <pow />
                        <apply>
                          <indexer />
                          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">ω</id>
                          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M</id>
                        </apply>
                        <apply>
                          <mult />
                          <id xml:space="preserve">m</id>
                          <id xml:space="preserve">p</id>
                        </apply>
                      </apply>
                    </apply>
                    <apply>
                      <pow />
                      <apply>
                        <indexer />
                        <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">ω</id>
                        <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">N</id>
                      </apply>
                      <apply>
                        <mult />
                        <id xml:space="preserve">n</id>
                        <id xml:space="preserve">p</id>
                      </apply>
                    </apply>
                  </apply>
                </parens>
              </lambda>
              <lowerBound>
                <real>0</real>
              </lowerBound>
              <upperBound>
                <apply>
                  <minus />
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">N</id>
                  <real>1</real>
                </apply>
              </upperBound>
            </apply>
          </lambda>
          <lowerBound>
            <real>0</real>
          </lowerBound>
          <upperBound>
            <apply>
              <minus />
              <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M</id>
              <real>1</real>
            </apply>
          </upperBound>
        </apply>
      </apply>
    </define>
    <resultFormat>
      <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

4. Compare the resulting inverse transform of matrix C with the output of the idft function.

Click to copy this expression

Click to copy this expression

The results are identical.