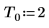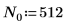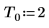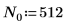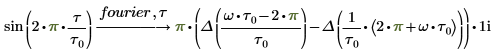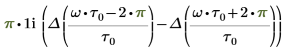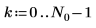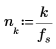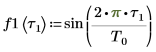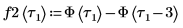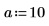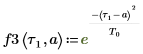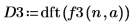Example: Fourier Transform Pairs
Define the period, the sampling frequency, and the number of samples of a signal.
Sinusoidal Signal
1. Use symbolic evaluation to find the Fourier transform of a sinusoidal signal.
Rearranging the terms of the result gives:
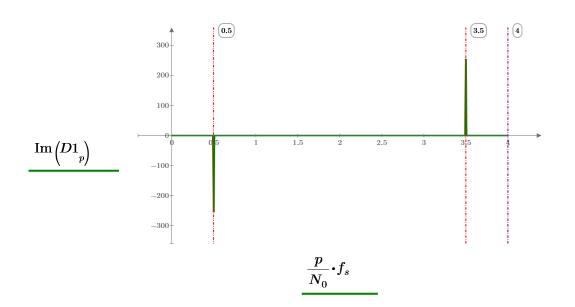
The result shows two components involving the Dirac delta (unit impulse) Δ function.
2. Use the sin function to define a sinusoidal signal.
3. Plot the first few elements of function f1.
4. Use the dft function to find the Discrete Fourier Transform of the signal.
5. Plot the two components of the Fourier Transform of the function. Use vertical markers to show where they occur relative to the sampling frequency.
Square Pulse (boxcar) Signal
1. Use the Heaviside step function Φ to define a square pulse signal.
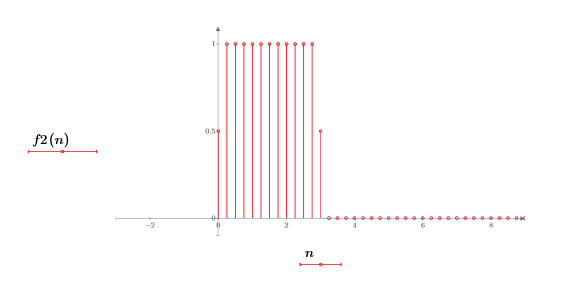
2. Plot the first few elements of function f2.
3. Use the dft function to find the discrete Fourier transform of the square pulse signal.
4. Plot the Fourier Transform of the square pulse signal. Use vertical markers to show where they occur relative to the sampling frequency.
Gaussian Signal
1. Define the following Gaussian signal.
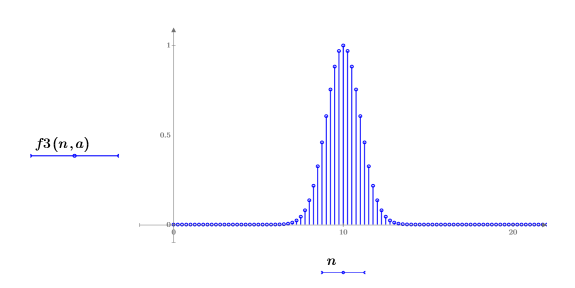
2. Plot the first few elements of function f3.
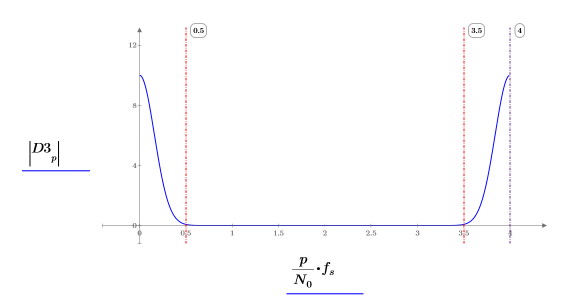
3. Use the dft function to find the discrete Fourier transform of the Gaussian signal.
4. Plot the Fourier Transform of the Gaussian signal. Use vertical markers to show where they occur relative to the sampling frequency.