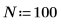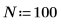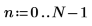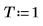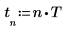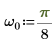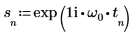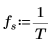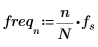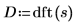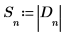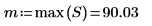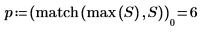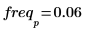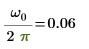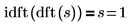Example: DFT of Complex Functions
Use the dft and idft functions to compute the complex or real forward or inverse Fourier Transforms.
1. Create some simulated complex data with N data points.
2. Define the sampling spacing.
3. Use the exp function to define the following signal.
4. Define the sampling frequency and the frequency corresponding to the nth entry in the transformed vector.
5. Apply the dft function to transform the data to the frequency domain.
6. Save the magnitude of elements of array D into a new array.
7. Use the match and max functions to calculate the amplitude and frequency of the peak.
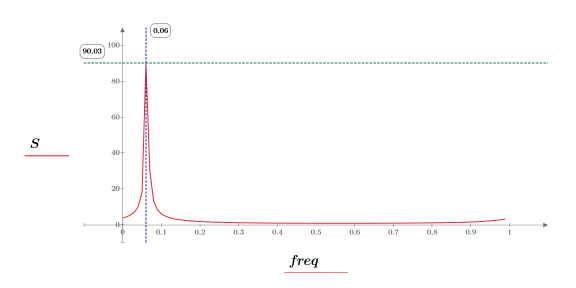
8. Plot the magnitude of DFT as a function of frequency.
9. Show that the frequency of the peak corresponds to ω0/2π.
10. Use the idft function to show that the IDFT of DFT of a signal returns the signal itself.