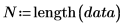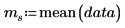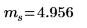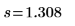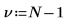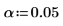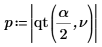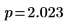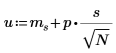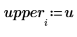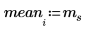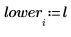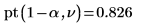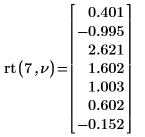Example: Confidence Interval for the Mean
Calculate a confidence interval for an estimate of the mean of a normal population when the population variance is unknown.
1. Define a sample data set.
2. Use functions length, mean and stdev to collect the sample statistics.
Number of samples | | |
Sample mean | | |
Sample standard deviation | | |
Degrees of freedom | | |
3. Enter the two-tailed significance level:
This is equivalent to a 95% confidence interval.
4. Use function qt to calculate the 95th percentile of the Student t-distribution for a two-tailed test.
5. Calculate the lower and upper limits of the confidence interval.
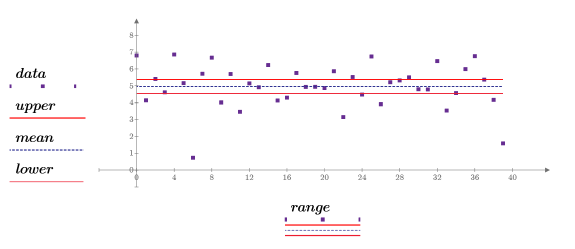
6. Plot the sample data, its mean and confidence interval.
7. Use function pt to calculate the cumulative probability distribution for the confidence interval:
8. Use function rt to create a vector of random numbers having a Student's t-distribution:
Recalculating the worksheet causes function rt to return a different set of random numbers.