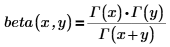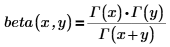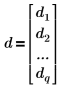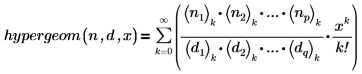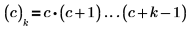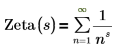Beta, Hypergeom and Zeta
• beta(x, y)—Returns the beta function, which is defined in terms of the gamma function Γ(x) as follows:
• hypergeom(n, d, x)—Returns the hypergeonometric function. The hypergeometric function of order p, q for vectors n and d is defined as follows:
where (c)k is the rising factorial defined as:
• Zeta(s)—Returns the Riemann zeta function, which is defined as follows:
Arguments
• x is a real or complex scalar.
• y is a real or complex scalar.
• n is a column vector.
• d is a column vector.
• s is a real or complex scalar.
Additional Information
The beta, hypergeom, and Zeta functions can only be evaluated symbolically.